使用 Tensorflow 极简实现线性回归
文章目录
应工作之要,最近在看机器学习。虽然机器学习挺火的,然而好的机器学习教程真的少,不少是掐住了人们急功近利的心态,提供各种“一口吃成个胖子”的“食谱”。我也是品尝了许多,现在隐隐约约看出点门道来。入门机器学习,不等于入门深度学习,初学者没必要一开始深扎到学术前沿去,而且不少像我这样的开发者更习惯从用出发,像机器学习这种原理性较强的工程,我们就很吃亏了。比起如何提供更好的算法,我们更关心如何针对现有问题利用现有算法解决问题。虽然相关的包已经很多了,但一些特殊需求还是驱使我们去学习 Tensorflow 以特异化我们的工程。
闲话少说,讲讲线性回归的实现。首先先明确的一点就是,线性回归就是线性神经网络。其次,我假设你是懂原理的,但是不清楚如何用 Tensorflow 实现。我们实际上是可以通过原理,视 Tensorflow 为工具集以实现一个最简的神经网络。
数据准备
import matplotlib.pyplot as plt
import tensorflow as tf
true_w = 10.9
true_b = 20.0
num_samples = 100
X = tf.random.normal(shape=[num_samples, 1]).numpy()
noise = tf.random.normal(shape=[num_samples, 1]).numpy()
y = X * true_w + true_b + noise
true_w 和 true_b 是我们真正要求取的结果。
线性回归的一般模型是一元一次函数。
最简(陋)的实现
建立模型
class Model(object):
def __init__(self):
self.W = tf.Variable(tf.random.uniform([1]))
self.b = tf.Variable(tf.random.uniform([1]))
def __call__(self, x):
return self.W *x + self.b
model = Model()
我们建立了一个线性模型,此刻它的 W 和 b 为随机值。
定义损失函数
def loss(model, x, y):
_y = model(x)
return tf.reduce_mean(tf.square(_y - y))
这里实现了平方损失函数。 $$ Loos(w, b, x, y) = \sum_{i=1}^N(f(w,b,x_i)-y_i)^2 $$
训练
epochs = 10
learning_rate = 0.1
for epoch in range(epochs):
with tf.GradientTape() as tape:
losses = loss(model, X, y)
dW, db = tape.gradient(losses, [model.W, model.b])
model.W.assign_sub(learning_rate * dW)
model.b.assign_sub(learning_rate * db)
print(f'Epoch [{epoch}/{epochs}], loss [{losses:.3f}], W/b [{float(model.W.numpy()):.3f}/{float(model.b.numpy()):.3f}]')
plt.scatter(X, y)
plt.plot(X, model(X), c='r')
这部分代码就是在自动求导寻求梯度。
with tf.GradientTape() as tape:
losses = loss(model, X, y)
dW, db = tape.gradient(losses, [model.W, model.b])
然后更新梯度。
更新次数到达一定程度,梯度将不会再更新了。
查看结果
plt.scatter(X, y)
plt.plot(X, model(X), c='r')
借助 matplotlib 我们可以查看我们的结果。
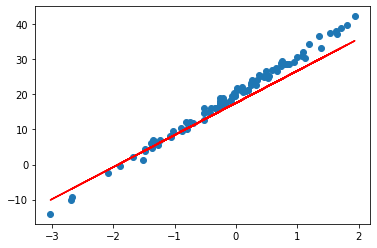
可以看到我们的结果非常贴近了。训练并不意味着非要特别多才管用,训练到一定程度就无效了,我们实际上只是在逼近我们想要的那个结果。
使用 Tensorflow 高阶 API 改进
建立模型
model = tf.keras.layers.Dense(units=1)
这里我们使用线性神经元来处理,此时的 model 是一个神经元。
梯度下降
epochs = 100
learning_rate = 0.02
for epoch in range(epochs):
with tf.GradientTape() as tape:
_y = model(X)
loss = tf.reduce_mean(tf.keras.losses.mean_squared_error(y, _y))
grads = tape.gradient(loss, model.variables)
optimizer = tf.keras.optimizers.SGD(learning_rate)
optimizer.apply_gradients(zip(grads, model.variables))
print(f'Epoch [{epoch}/{epochs}], loss [{loss:.3f}]')
损失函数是与之前一样的写法,但是我们借助了 keras 已经实现的方法。 optimizer 用的是 SGD ,即随机梯度下降,也称为增量梯度下降,是一种迭代方法,用于优化可微分目标函数。该方法通过在小批量数据上计算损失函数的梯度而迭代地更新权重与偏置项,这里其实就是之前实现的那个更新。
梯度下降算法需要根据不同情况下调整,目前我们就需要用这个。
查看结果
与之前一样的代码。

这里需要注意一下学习次数和学习率,有时候结果不够可能是训练次数不够,但如果训练太慢的话可以尝试调整一下学习率,不过不要调过头。调参是一门学问。
最简实现——利用 Tensorflow 线性神经网络
建立模型
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(units=1, input_dim=1))
这里我们建立而一层的、且只包含一个神经元的线性神经网络。 tf.keras.Sequential() 代表神经元线性排布。
关于结构,可以使用 model.summary() 查看。
训练
model.compile(optimizer='sgd', loss='mse')
model.fit(X, y, steps_per_epoch=1000)
代码简化了非常之多,因为代码本来重复性就特别高。 compile 我们将编译模型,并加入优化器和损失函数, sgd 和 mse 指代的就是我们之前的方法。 fit 就是正式训练开始,将会训练 1000 。
代码整体非常的自动化,也非常简洁。这就是使用 Tensorflow 的好处。
查看结果
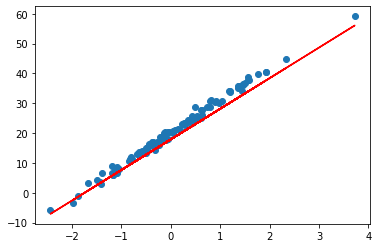
可以根据结果再调整训练。
说实话,图形化也是机器学习非常重要的一环,图片能直观的将一些关系表达出来。所以,善用 plt 。
结语
目前学习机器学习也一段时间了,感觉最难的部分倒也不是数学,而是缺乏引导。
我读的不少文章,要么讲得太初级,要么太高级,要么过于理论,要完全把内容照抄一遍,只能说他们懂了,我完全没有懂。所以与其等待别人,不如自己想办法。
个人学下来,目前觉得,得至少把机器学习常用的三大基础框架学了首先,其他的再徐徐图之。 Tensorflow 方面深度学习过于出名了,反而不利于初学机器学习的人,我觉得一开始进行机器学习就碰神经网络简直劝退。理论上,用 Tensorflow 进行机器学习也是可以的,然而很少有人做,我表示也是很难受,只能一个个找。我要是真做成了,就分享给大家,哈哈!
附录
文章作者 bigshans
上次更新 2021-11-05
